La proportionnalité – Boss'En Math

Tous les jours, nous rencontrons des situations où évoluent des grandeurs. Le cas de grandeurs parfaitement proportionnelles est rare au quotidien.

En cas de proportionnalité, le retour à l’unité est une méthode simple et très efficace pour résoudre de nombreux calculs.

Dans l’univers mathématique, il existe de nombreuses relations de proportionnalité, plus ou moins célèbres.

Découvrons …

Divisons 41,35 € par 44,99. Nous obtenons 0,919 €. C’est le prix d’un litre. Et si nous divisons 44,99 Litres par 41,35 ?

Le pack de 6 bouteilles de 1,5 L chacune vaut 7,80 €. Quel est le prix de 8 bouteilles ?

Le 16 août 2009, Usan Bolt a couru le 100 mètres en 9,58 secondes. Quelle a été sa vitesse moyenne ?

30 % c’est 30 pour 100 ! Que cela signifie-t-il ?

Pour faire 15 crêpes, il nous faut 60 cL de lait, 300 gr de farine et 3 œufs. Et pour 40 crêpes ?

1/650 est l’échelle de cette maquette. Elle est donc 650 fois plus petite que la vraie Tour Eiffel. Quelle est la hauteur de cette maquette ?

Une goutte tombe toute les 4 secondes. Faut-il réparer ce robinet ?

Ma vitesse moyenne est de 3,3 km / h. Mon allure moyenne est de 17 : 34 min / km. Ces résultats sont-ils cohérents ?

Le Général Sherman a une circonférence de 31,3 m. Quel est son diamètre ?

Dans la langue française, la fréquence de la lettre e est de 12%. Qu’en est-il dans ce poème ?

J'ai lancé 100 fois le dé à 6 faces. J’ai obtenu 16 fois le chiffre 1. Soit une fréquence de 0,16. quelle serait la fréquence du 1 pour 100 000 lancés ?

Parmi tous les formats d’écran, le ratio le plus courant est de 9 : 16. Qu’en est-il de votre téléphone ?

Passez sur chaque photo et découvrez la question associée à chaque situation issue du quotidien.

Que retenir ?

La division permet de ramener une quantité à 1 unité.
Cela suppose une situation de proportionnalité.
C’est le retour à l’unité.

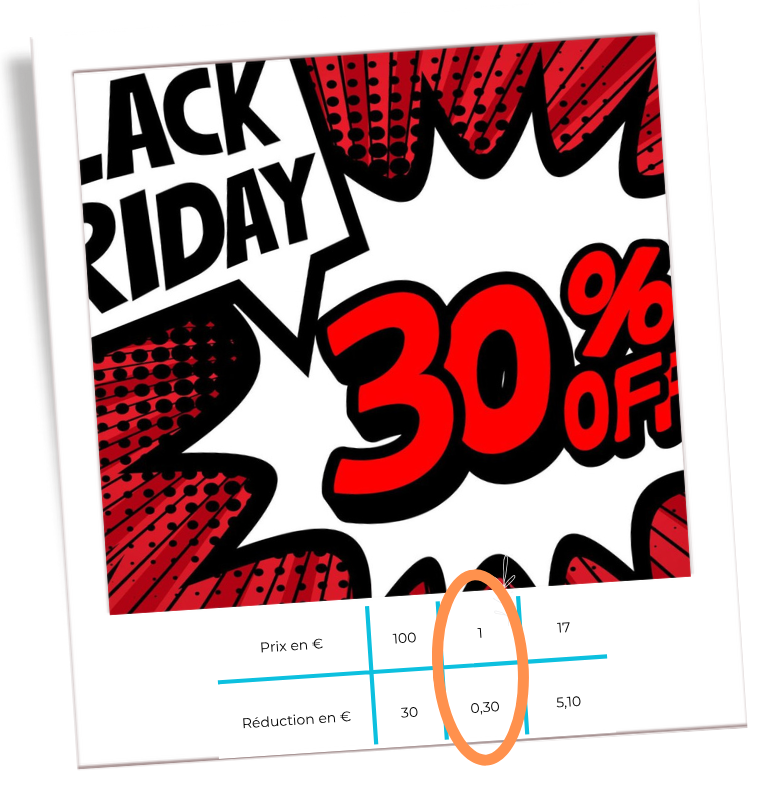
Un pourcentage
est un retour à 100 !

Que savoir ?

Une grandeur est quelque chose que l’on peut mesurer.

Une grandeur s’exprime dans une ou plusieurs unités.
Il ne faut pas confondre la grandeur et son unité de mesure.

Deux grandeurs sont proportionnelles lorsqu’elle sont reliées par un coefficient multiplicatif, constant et non nul.
C’est le coefficient de proportionnalité.

Le prix est proportionnel au volume d’essence.
la quantité d’eau pour éteindre un incendie n’est pas proportionnel à la durée du feu.

La circonférence d’un cercle est parfaitement proportionnelle
à son diamètre.

Dans le cas de 2 grandeurs proportionnelles, le retour
à l’unité et la multiplication permettent de calculer
n’importe quelle quantité à partir de valeurs connues.
C’est la méthode de la règle de trois.

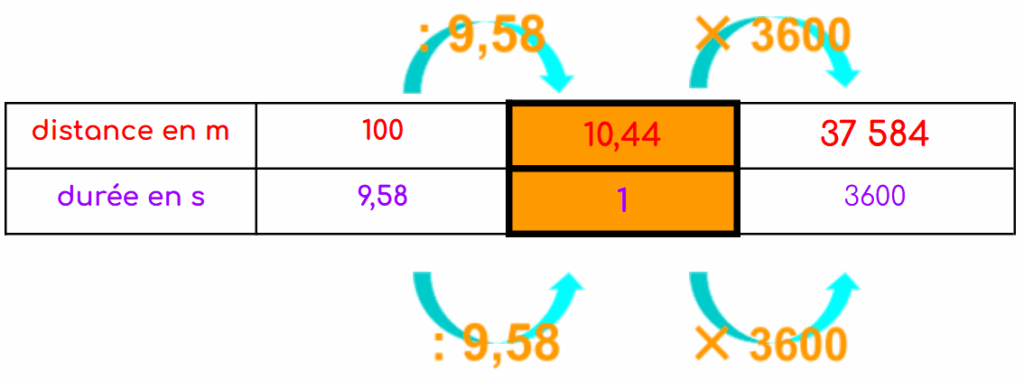
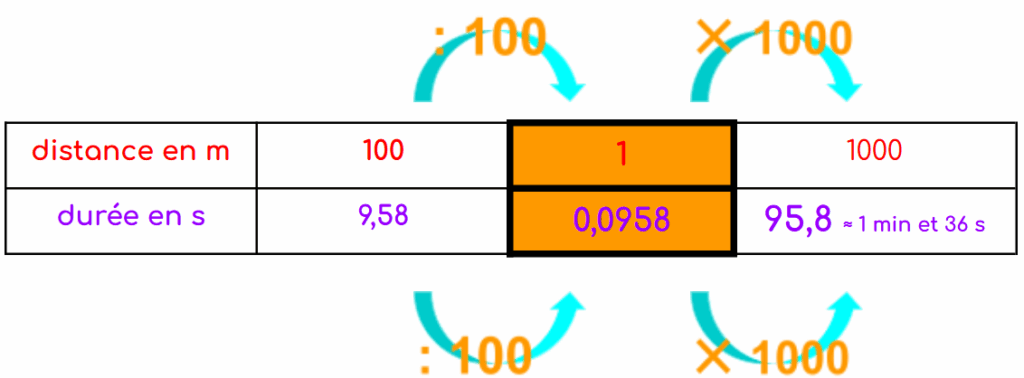
V_Bolt = 37,584 km/h

A_Bolt = 95,8 s/km

ATTENTION !

Ne pas confondre la règle de trois et le produit en croix.
En période d’apprentissage, le produit en croix est très déconseillé.
En effet, le produit en croix est un truc qui fonctionne mais qui est vide de sens.

En bonus

https://lesfondamentaux.reseau-canope.fr:/embed/video/decouvrir-la-proportionnalite