
Qui n’a jamais rêvé d’atteindre l’inaccessible ?
Par exemple, mesurer une hauteur sans la parcourir.
La méthode mise en jeu est finalement assez simple. Mais elle est terriblement efficace !
Découvrons …
Nous sommes au Moyen-âge.
Nous allons attaquer la Tour de ce château-fort.
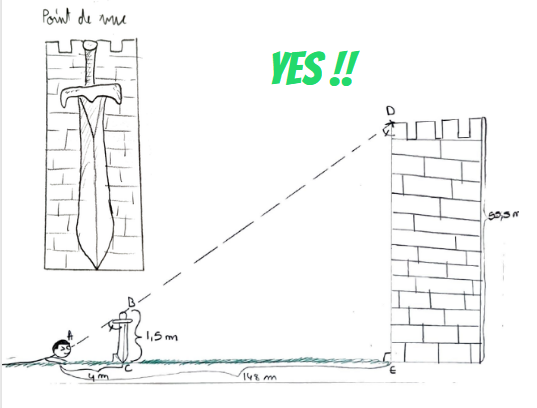
Afin de régler notre catapulte, il nous faut connaître la hauteur de La Tour.
Mais impossible de s’en approcher …

… et les mesures que vous pourriez obtenir sur le terrain.
PS : la corde est graduée.



Raisonnement

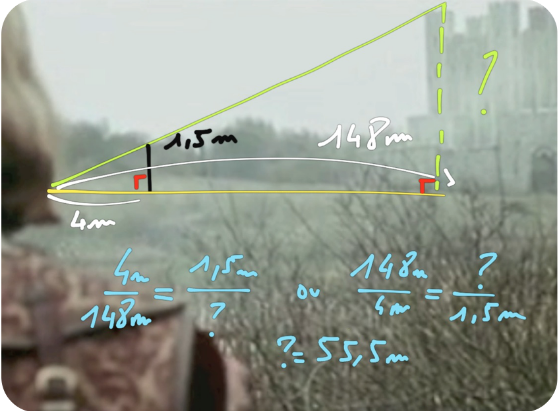
On obtient deux triangles rectangles.
Ils ont les mêmes angles, mais ils n’ont pas la même taille.
Le grand triangle est 37 fois plus grand que le petit.
La Tour mesure 55,5 mètres de haut.
distances fournies en classe et raisonnement réalisé et rédigé par un groupe d’élèves de 4e.
Que retenir ?
Le recours à deux triangles
nous a permis de calculer
ce que l’on ne peut mesurer.
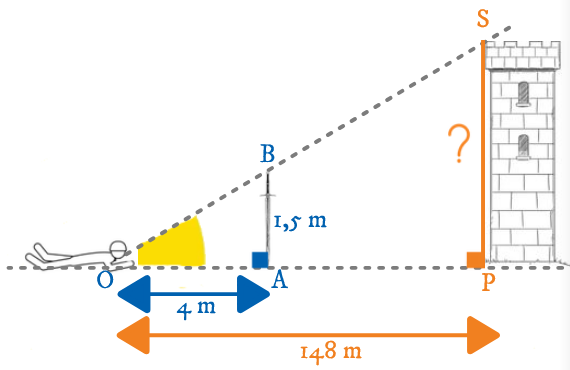
Les point O, A et P sont alignés.
Les point O, B et S sont alignés.
Les droites (AB) et (PS) sont parallèles.
Donc, Les triangles OAB et OPS
ont les mêmes angles.
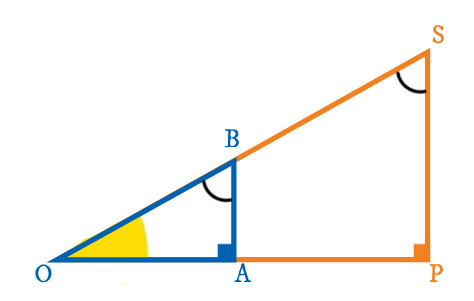
Ils sont semblables.
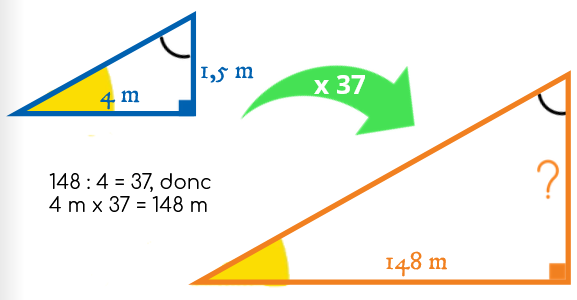
Le triangle OPS est 37 fois plus grand que le triangle OAB.
Donc,
? = 1,5 m x 37
La Tour mesure
55,5 mètres de hauteur.

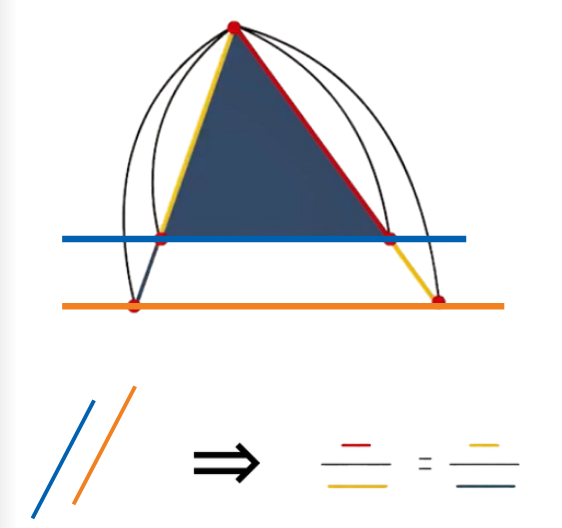
Le parallélisme et l’alignement des points forment une configuration composé de 2 triangles semblables :
Ils ont les mêmes angles mais sont de taille différente.
Le rapport des longueurs y est conservé.
Que savoir ?
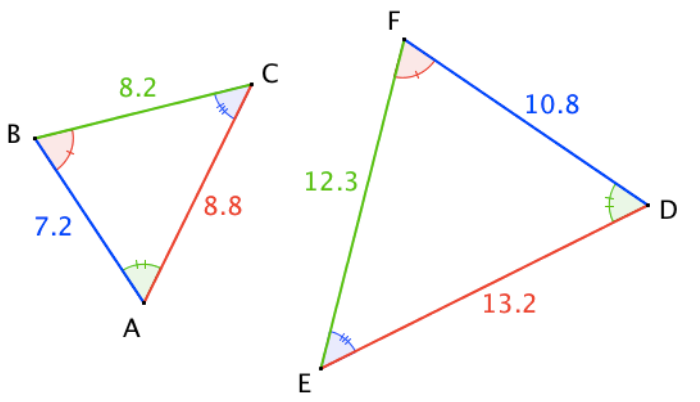
Définition : Deux triangles sont semblables lorsque leurs angles sont de même mesure.
Propriété : Deux triangles semblables ont leurs côtés homologues proportionnels.
Si deux droites sécantes croisent deux droites parallèles,
alors on peut trouver une mesure manquante,
à partir de côtés connus.
Aujourd’hui en France,
cette propriété porte le nom
d’un Mathématicien célèbre.
On parle du Théorème de Thalès.
Pourtant, ce sont juste des triangles semblables.
A trois, on est plus fort !
En bonus
